고정 헤더 영역
상세 컨텐츠
본문
'거리'로 등식을 세우는 유형
거리를 기준으로 삼아서 식을 쓰는 대표적인 유형이 바로 두 사람이 운동장이나 호숫가를 도는 유형이에요.
항상 두 사람이 등장하고, 운동장이라든지 호수와 같은 장소가 등장해요.
이때 두 사람이 '동시에' 출발을 하고 '반대방향'으로 걷기 시작할 때, 두 사람이 만날 때까지 걸린 시간을 물어보는 문제가 가장 기본문제예요.
두 사람 A, B가 둘레의 길이가 3km인 호숫가를
같은 지점에서 동시에 출발하고 반대방향으로 걷기 시작할 때,
A는 분속 50m, B는 분속 30m의 속력으로 걷는다면,
두 사람이 만날 때까지 걸린 시간은?

그러면 분명 두 사람은 중간 어디즘에서 만나겠죠?

두 사람이 만나는 그때(x)까지 걸린 시간을 물어본다면 '시간으로 식을 세워야 하나?' 라고 잘못 생각할 수 있어요.
이 문제는 각자 '움직인 거리'에 초점을 맞춰야 해요. 그림을 잘 보면 A가 움직인 경로와 B가 움직인 경로 두 가지를 합치면 호수의 둘레의 길이와 같아진다는 것을 알 수 있어요.
A가 움직인 거리 + B가 움직인 거리 = 호수의 둘레의 길이
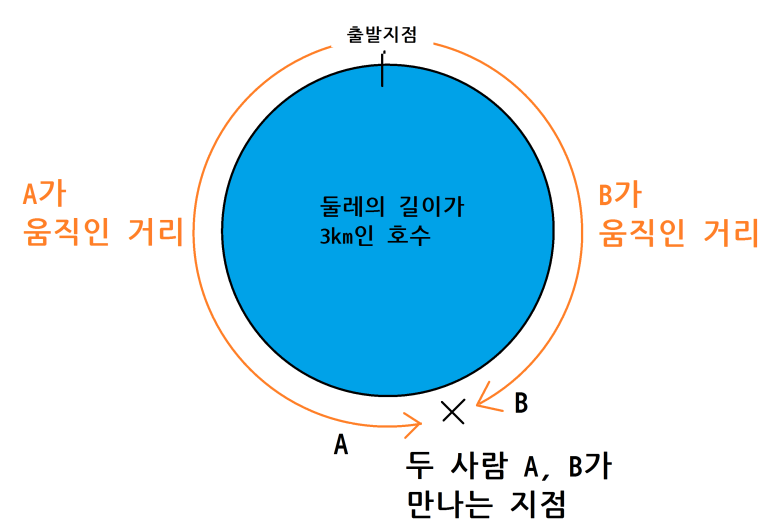
A가 움직인 거리를 식으로 나타내는 부분만 하면 이 식은 완성이에요.
거리 = 시간 × 속력
이므로 시간은 미지수 x, A의 속력으 분속 50m 이므로
A가 움직인 거리 = 50x
같은 방법으로 B는 동시에 출발했으니 같은 시간 x 동안 분속 30의 속력으로 움직였으므로
B가 움직인 거리 = 30x
호수의 둘레의 길이는 3km 이므로 3000m로 바꿔주면(단위를 바꾸는 이유는 분속이 m단위이기 때문에 동일한 단위로 맞춰주기 위해서예요)
50x + 30x = 3000
80x = 3000
x = 37.5
정답은 37.5분이예요.

'중등 프린트 학습지' 카테고리의 다른 글
| 중1 수학 > 소인수분해 > 합성수 찾기 프린트 (0) | 2022.10.19 |
|---|---|
| 중1 수학 > 소인수분해 > 소수 찾기 문제 (0) | 2022.10.19 |
| 중3 수학 > 피타고라스의 정리 증명법 (0) | 2022.10.17 |
| 중2 수학 > 단항식의 계산 > 지수법칙(1~2번) + 프린트 학습지 (0) | 2022.10.13 |
| 중1 수학 > 일차방정식의 활용 > 원가, 정가, 이익의 개념 (0) | 2022.10.13 |





