고정 헤더 영역
상세 컨텐츠
본문
지수법칙에 대해서 알아보도록 할게요.
지수란 어떤 수나 문자를 여러 번 곱하는 경우에 식을 간단히 나타내는 방법입니다.
가령, 3을 네 번 곱하는 식을 간단히 나타낸다면 다음과 같아요.

여기서 3이 4를 짊어진 것 같은 모양이 바로 3을 4번 곱한 수라는 뜻이에요.
만약 어떤 문자 a를 5번 곱한 수라면,

이렇게 나타낼 수 있는 거에요.
그럼 이런 경우는 어떻게 해석할 수 있을까요?

a를 2번 곱한 수와 a를 3번 곱한 수를 곱하면 a가 총 몇 번 곱해진 것일까요.

결국 a를 다섯번 곱한 수이므로 □에는 5가 들어가는 것이죠.
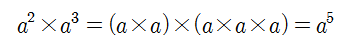
그렇다면 다음 은 어떨까요?
a가 세 번 곱해지고 b가 2번 곱해진 수를 간단히 나타내려면

a는 a의 세 제곱, b는 b의 제곱으로 나타낼 수 있어요.
지수를 읽는 방법은
지수가 2면 제곱, 3이면 세 제곱, 4이면 네 제곱... 이라고 하기도 하고
또는 지수가 2면 2승, 3이면 3승, 4이면 4승이라고 해요.
그러면 위의 경우는 a의 3승(또는 세 제곱), b의 2승(또는 제곱)으로 읽을 수 있고 다음과 같이 표현해요.

그렇다면 이제 지수의 표현방법과 읽는 법을 알았으니, 이것을 공식화해보기로 해요.
만약 어떤 문자 a를 m번 곱한 수와 n번 곱한 수를 곱하게 되면 다음과 같아요.

결국 나란히 지수꼴이 있을 경우에는 지수끼리 더하는 게 된답니다.
그럼 지수법칙 중 하나에 대해 살펴보았는데요,
이번에는 지수의 나눗셈에 대해 살펴볼게요.
만약 다음과 같은 식이 있다고 한다면 어떻게 될까요.

a를 6번 곱한 수에서 a를 2번 곱한 수를 나누는 식인데요, 나눗셈을 곱셈으로 바꾸고 역수를 취하면, 다음과 같아요.

a의 6승은 분자, a의 2승(제곱)은 분모가 되므로 식을 정리해보면 약분을 할 수 있는 식이 돼요.
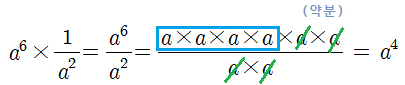
약분을 하고도 남은 부분이 남는 식이 되는거죠. 이 문제는 분자쪽에 a가 4개가 남았으므로 a의 4승이 되었습니다.
그럼 분모가 더 남는 경우의 식도 있을까요? 다음 식을 볼게요.

아까와 다르게 오른쪽의 수의 지수가 왼쪽보다 큰 경우예요. 이것도 마찬가지로 분수로 나타내어 계산해보면,
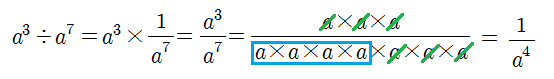
분모쪽의 a가 약분하고 나서도 더 남는 경우에는 분자는 1이 되고 분모가 a의 4승이 돼요.
원리는 분수꼴로 나타내고 약분시킨다는 같은 원리예요.
자 그럼 이것을 공식으로 만들면 어떻게 될까요.
a를 m번 곱한 수에 a를 n번 곱한 수를 나누게 되면

이때 m과 n의 대소관계에 따라 세 가지 경우가 생겨요. 약분을 하고 났을 때, m이 크면 분자쪽에 a가 남게 되고, n이 크면 분모쪽의 a가 남게 되는 경우, m과 n이 같으면 모두 약분되어서 1이되는 세 가지 경우로 나뉘게 돼요.

여기까지 잠깐 정리를 해볼게요.

두 가지 지수법칙에 대해서 살펴봤어요. 나머지 지수법칙은 다음 포스팅에서 다루도록 할게요.
미리보기 > 중2 단항식의 계산 - 지수법칙 (덧셈과 나눗셈)
'중등 프린트 학습지' 카테고리의 다른 글
| 중1 수학 > 일차방정식의 활용 > 거리, 속력, 시간 문제① - '거리'가 등식의 기준인 문제유형 (0) | 2022.10.17 |
|---|---|
| 중3 수학 > 피타고라스의 정리 증명법 (0) | 2022.10.17 |
| 중1 수학 > 일차방정식의 활용 > 원가, 정가, 이익의 개념 (0) | 2022.10.13 |
| 중1 수학 > 일차방정식의 활용 > 소금물 문제(소금물에 소금 더 넣기) + 프린트 학습지 (0) | 2022.10.11 |
| 중1 수학 > 일차방정식의 활용 > 소금물의 농도, 소금의 양 공식과 원리 (0) | 2022.10.11 |







