고정 헤더 영역
상세 컨텐츠
본문
중등 1학년 수학 > 원과 부채꼴 > 부채꼴의 색칠된 부분의 둘레 구하기
이번 문제는 부채꼴에서 색칠된 부분의 둘레를 구하는 문제입니다. 주어진 조건을 바탕으로 색칠된 부분의 둘레를 계산보겠습니다.
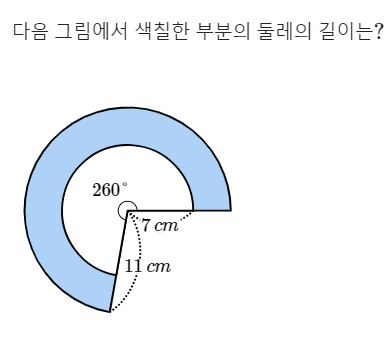
문제 설명:
- 조건 1: 주어진 부채꼴의 중심각은 \(260^\circ\)입니다.
- 조건 2: 큰 부채꼴의 반지름의 길이는 \(11 \, cm\)입니다.
- 조건 3: 작은 부채꼴의 반지름의 길이는 \(7 \, cm\)입니다.
- 목표: 주어진 조건을 바탕으로 색칠된 부분의 둘레를 구하세요.
문제 풀이:
이제 주어진 조건을 바탕으로 문제를 풀어보겠습니다.
- 먼저, 큰 부채꼴과 작은 부채꼴의 호의 길이를 각각 구해보겠습니다.
- 큰 부채꼴의 호의 길이는 \( \dfrac{260^\circ}{360^\circ} \times 2\pi \times 11 \, cm \) 입니다.
- 작은 부채꼴의 호의 길이는 \( \dfrac{260^\circ}{360^\circ} \times 2\pi \times 7 \, cm \) 입니다.
계산을 통해 각 호의 길이를 구해보면:
\[ \text{큰 부채꼴의 호의 길이} = \dfrac{260^\circ}{360^\circ} \times 2\pi \times 11 = \dfrac{260}{360} \times 22\pi = \dfrac{143}{9}\pi \, cm \]
\[ \text{작은 부채꼴의 호의 길이} = \dfrac{260^\circ}{360^\circ} \times 2\pi \times 7 = \dfrac{260}{360} \times 14\pi = \dfrac{91}{9}\pi \, cm \]
이제, 색칠된 부분의 둘레는 큰 부채꼴의 호의 길이와 작은 부채꼴의 호의 길이의 합, 그리고 큰 반지름과 작은 반지름의 차이로 계산됩니다:
\[\text{색칠된 부분의 둘레} = \left(\dfrac{143}{9}\pi + \dfrac{91}{9}\pi\right) + 2 \times (11 - 7) \, cm\]
계산하면,
\[\text{색칠된 부분의 둘레} = \dfrac{234}{9}\pi + 8 = 26\pi + 8 \, cm\]
따라서, 정답은 \((26\pi + 8)\) cm입니다.
더 많은 문제를 풀어보고 싶다면, 아래 링크에서 '모두매쓰' 사이트를 방문해 보세요!
www.modoo-math.com
모두매쓰 - 무제한으로 만들어지는 인공지능 수학 문제 생성 서비스
모두매쓰는 수학 문제 학습지를 무제한으로 생성하고 화면에서 즉시 풀 수 있도록 제공하는 인공지능 서비스입니다. 초등, 중등, 고등 교과서에서 다루는 핵심적인 문제들을 다양하게 제공하며
www.modoo-math.com
'중등 프린트 학습지' 카테고리의 다른 글
| 중등 1학년 수학 > 입체도형의 겉넓이와 부피 > 원뿔대의 겉넓이 계산 (0) | 2024.08.14 |
|---|---|
| 중등 1학년 수학 > 원과 부채꼴 > 부채꼴의 색칠된 부분 넓이 구하기 (0) | 2024.08.14 |
| 중등 1학년 수학 > 소인수분해 > 200 이하 자연수에서 기약분수 조건 구하기 (0) | 2024.08.14 |
| 중등 수학 프린트: 성공적인 학습을 위한 필수 도구와 모두매쓰의 특별한 서비스 (0) | 2024.08.13 |
| 중등 2학년 수학 > 무게중심과 넓이 > 삼각형의 넓이 구하기 (0) | 2024.08.13 |




