고등 수학 > 수학II > 정적분의 혁신적인 원리

고등 수학 > 수학II > 정적분 > 적분 탄생의 비밀, 기하학의 마법

오늘은 적분 탄생의 비밀을 얘기할까해요.

결론부터 말씀드리면 적분이 사실은 하나의 수를 기하학적 개념을 이용하여 탄생하게 되었다는 내용입니다.

그럼 본론으로 넘어가 이야기를 해볼게요. 다음과 같은 선분이 하나 있다고 해볼게요.

길이가 16인 선분이 하나 있다고 하겠습니다. 단위는 생략하도록 할게요. 16이라는 수를 우리는 어떻게 바라보고 있나요? 네, 여기서는 바로 '길이'로 바라보고 있어요.

​

16이라는 수를 '넓이'로 바라보면 어떻게 될까요?

길이가 16인 선분에서 넓이가 16인 직사각형 모양으로 바뀌었어요.

이렇게 16이라는 수를 '길이'로 볼 수도 있고, '넓이'로 볼 수도 있어요. 둘다 16이라는 수에 집중한다면 다르지 않아요.

​

하나의 수를 놓고, '길이'와 '넓이'를 왔다 갔다 할 수 있다는 것을 미분과 적분에서 이용하고 있다는 사실을 아시나요?

왜 그런지 다음 그림을 보면서 설명해볼게요.

​

 

위 그림은 '적분'이라는 개념을 배울 때 등장하는 전형적인 문제 상황이에요. 파란색으로 칠해진 부분의 넓이를 구하기 위해 보통 교과서에서는 다음과 같은 설명을 하는데요,

파란색의 부분을 잘게 잘게 쪼개어 직사각형 형태로 만들고, 직사각형의 넓이를 모두 더하면 구하고자 하는 넓이에 가까워지는데, 만약 무한히 잘게 쪼갠다면 오차가 0에 수렴해서 실제로 넓이를 구할 수 있게 된다고 말이죠.

​

이보다 더 직관적이고 훌륭한 설명이 과연 있을까요? 그렇기 때문에 교과서에서는 '구분구적법'이라는 이름으로 적분에 대한 개념을 가르친답니다. 구분구적법이란 구분 -> 영역을 잘게 구분지어서, 구적법 -> 더하여 값을 구하는 방법. 이라는 뜻이죠.

​

그런데 말이죠. 이 설명은 왜 우리가 정적분을 계산할 때, 원시함수를 이용하는지에 대한 설명이 되지 않아요. 특히 넓이를 계속 넓이로만 바라보고 있다는 거에요. 다시 말해 기하학적 모델이 변하지 않았어요.

​

 

기하학적 전환 = 발상의 전환

​

만일 누군가가 도형의 넓이를 구하려고 하는데 도형을 이리저리 재거나 자르지 않고 길이로 만들어버려서 값을 구한다고 생각해보세요. 그것을 최초로 생각한 사람이 있다면 정말로 대단하고도 혁신적인 발상이 아닐 수가 없는데요

​

앞서 처음에 넓이를 길이로 볼 수도 있고, 길이를 넓이로 볼수도 있다고 했죠? 그렇다면 우리는 위 파란색 영역의 '넓이'를 '길이'로 바라보면 문제를 해결할 수 있어요.

그 방법에 대해서 이야기할게요. 여기서부터는 약간의 수식이 포함되지만, 수식보다는 수를 보는 관점의 변화가 어떻게 미분과 적분에 내포되어 있는지에 포커스를 맞춰주시길 바래요.

​

우선, 아까 보았던 y=f(x) 라는 함수를 부정적분한 함수 y=F(x)를 찾아요.

그리고 x의 값이 b일 때의 함수값 F(b)에서 x의 값이 a일 때의 함수값 F(a)를 뺀 F(b)-F(a)로서 넓이를 구하게 된답니다. 어떻게 이것이 가능한 걸까요?

이 질문에 대한 답을 하려해요.

​

드디어 인테그랄이라는 수식이 등장할거에요. 그리고 파란색 영역의 넓이를 다음과 같이 식으로 표현해요.

​

인테그랄은 x가 a에서부터 출발해 b까지 f(x) 함수와 x축 사이에 있는 영역의 값을 구하는 하나의 표현이랍니다.

저 식을 잘 보면, f(x) 옆에 dx 라는 이상한 글자가 있어요. 이게 도대체 뭘까요?

 

dx라는 것은 delta x 의 줄임말이에요. delta란 '변화하는 양'을 뜻해요. 그러니 dx는 x의 변화량을 말하는 거랍니다. 그럼 dx말고도 세모 모양으로 된 Δx라고 나타내도 되었을텐데 왜 dx라고 한 것일까요.

보통 Δx 와 dx는 약간 차이가 있어요. 특히 dx란 0에 한없이 가까운 값으로서의 변화량을 말합니다. 좀 작은 x의 폭 정도로 생각하면 될 거에요.

보통 수학에서는 수식의 좌우에 아무것도 없으면 '곱셈'의 생략으로 본답니다.

​

dx가 f(x)에 곱해졌다는 사실로부터 출발해야해요. f(x)dx가 과연 어디서부터 온 걸까요?

​

 

'넓이'야... 너의 부모는 사실 '길이'였단다.

​

f(x)dx 는 f(x) × dx 예요. 이 수식을 기하학적으로 해석해보면 직사각형의 넓이식으로 볼 수 있어요.

​

기하학적으로 바라보면 f(x)dx는 '직사각형 조각'인데요,

인테그랄 a부터 b까지 적분식은 바로 이런 '직사각형 조각'을 a부터 b까지 끌어모은 것을 뜻해요.

​

인테그랄은 x=a에서 x=b까지 이어질 때 만들어지는 수 많은 '직사각형 조각'의 연속하는 실수로서 합해지는 기능을해요. 연속이 무엇인지 정확히 몰라도 괜찮아요. 위 그림은 대략 열 몇번 구간을 나누었지만, 실제로는 수백만 수천만 아니 그 이상 잘게 쪼개어져 합해지게 된답니다.

​

여기까지는 f(x)dx는 '넓이'의 관점으로 수를 해석한 거에요. 그렇다면 넓이를 어떻게 길이로 생각할 수 있을까요?

아래 그림을 한 번 보도록할게요. 마법같은 일이 일어난답니다.

아래 함수의 그래프는 y=f(x)의 함수를 부정적분한 y=F(x)의 함수의 그래프예요. 만약 y=F(x)를 모든 실수 x에 대하여 미분을 하면 dy/dx 라는 그림을 생각할 수 있게 되요. 그리고 dy조각들이 무수히 많이 생기게 된답니다. dy를 모두 합하게 되면 F(b)-F(a)의 '길이'와 같아진다는 것을 직관적으로 알 수 있어요.

이게 f(x)dx와 무슨 관계가 있을까요? 그리고 dy의 합이 결국 우리가 찾고자 하는 '넓이'와 같다는 것을 어떻게 알 수 있을까요? 일단 위 그림에서 'dy의 합'을 인테그랄로 표현한 식을 보세요.

​

이 수식을 이해해야해요. dy란 y의 작은 변화량이에요. 그림에 보시면 dy가 무수히 많이 있고, dy를 모두 모으면 dy의 합이 F(b)-F(a)외 같다는 것을 알 수 있어요. 그런데, dy의 y는 무엇과 같죠? 네 F(x)와 같습니다. 그럼 다음과 같이 식을 만들 수 있겠습니다.

​

자 이제 거의 다 왔습니다. dF(x)가 무엇을 뜻하는지 아래 그림에서 다시 확인해봐요.

​

dF(x)는 연속하는 실수 x에 대하여 무수히 많아요. 그걸 모두 합한 게 dy의 합이며 F(b)-F(a)라는 사실을 계속 상기시켜주세요.

​

이제 마법같은 일이 벌어집니다. 아래 식을 보세요.

dx는 0이 아니기 때문에 분모에 올 수 있다는 것도 주의하시기 바래요. dx/dx를 곱하게 되면 1을 곱하는 것과 같기 때문에 위 식이 성립한다는 것은 자명해요.

그렇다면 이제 분모에 있는 dx를 다음과 같이 dF(x) 아래에 놓게 되면 신기한 현상이 발생합니다.

​

dF(x)/dx 의 의미를 발견하셨나요? 이것은 F(x)를 x에 관하여 미분한 식입니다. 따라서 f(x)와 같아요.

​

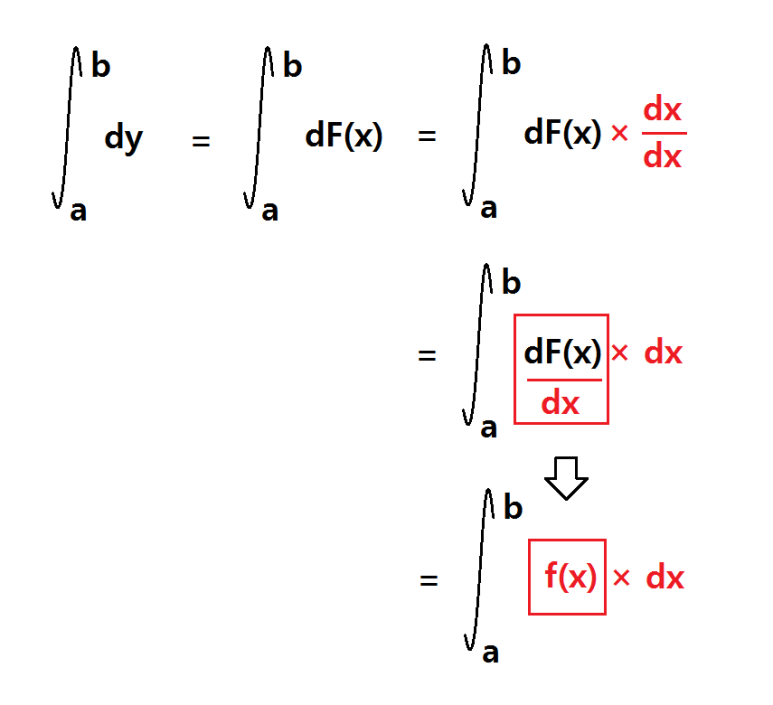
'길이'였던 dF(x)가 '넓이'인 f(x)dx가 되는 마법같은 일이 일어났습니다.

즉 dF(x)는 f(x)dx와 똑같은 값을 가진다는 사실을요.

그럼으로 나타내면 다음과 같아요.

​

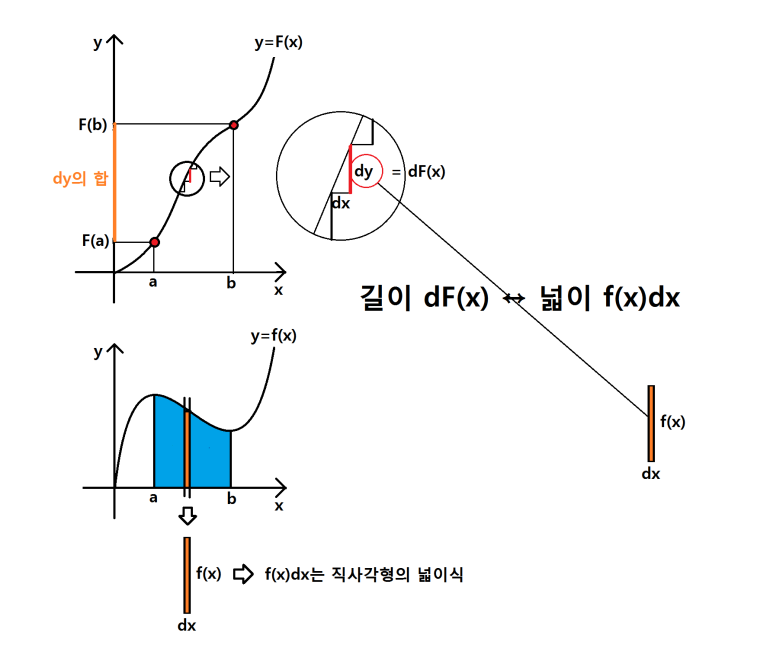
y=f(x)와 y=F(x)는 미분과 적분의 관계에 있는 식이고, y=F(x)의 y의 작은 변화조각인 dy=dF(x)가 미분함수인 y=f(x)의 그래프에서 볼 수 있는 f(x)dx라는 직사각형 조각과 동일한 값을 가지므로,

우리는 파란색 영역의 넓이를 원시함수의 함수값의 변화량으로 구할 수 있게 된 것입니다.

​

놀랍지 않나요? 복잡해보이는 곡선의 넓이를 '길이'라는 수학적인 개념으로 변환해서 구하게 된 것이요.

이 과정에서 인테그랄이라는 기호가 어떤 역할을 하는지도 더 자세히 알 수 있게 되었어요.

​

점, 선 면 등 기하학적인 모형이 미분과 적분에 얼마나 요긴하게 활용되는지 생각해보는 시간을 가졌으면 하는 바람에서 이만 글을 마치도록 하겠습니다.

​

그럼 좋은 하루되세요.

​