고정 헤더 영역
상세 컨텐츠
본문
고등수학 > 확률과 통계 > 확률의 뜻 > 3개의 점을 선택할 때, 삼각형이 만들어질 확률
3개의 점을 선택하여 연결할 때, 만들 수 있는 삼각형의 수를 묻는 문제를 풀도록 할게요.
이 문제를 '조합'의 개념을 이용하면 간단히 해결할 수 있답니다.
문제를 풀면서 설명하도록 하겠습니다.

우선 확률을 계산하려면 전체 경우의 수를 계산해야겠죠. 전체 20개의 점에서 임의로 3개의 점을 선택하면 다음과 같아요.

다음으로 3개의 점을 택하여 연결할 때, 삼각형이 만들어지려면 어떤 점들을 선택해야 할까요? 이 문제의 답은 '그렇다면 어떤 경우에 삼각형이 만들어지지 않을까?'라고 거꾸로 생각하는 겁니다. 왜냐하면 그게 더 찾기 쉽기 때문인데요,
즉, 임의로 3개의 점을 선택하여 연결할 때, 딱 두 가지 경우 밖에 없답니다.
1) 삼각형이 만들어진다. 2) 삼각형이 만들어지지 않는다.
1), 2)를 합하면 전체 경우의 수가 되므로, 2) 삼각형이 만들어지지 않는다의 경우의 수를 찾은 다음 전체에서 제외하면 바로 삼각형이 만들어지는 경우의 수가 됩니다.
그럼 어떻게 하면 3개의 점을 연결했을 때 삼각형이 만들어지지 않을까요? 바로 다음과 같은 경우예요.

어떤 가상의 선이 있다고 할 때, 그 선 위에 있는 점 3개를 선택하여 연결하면 삼각형이 만들어지지 않아요. 그렇다면 이런 경우의 수를 어떻게 하면 효율적으로 찾을까요?
선을 그었을 때, 같은 선 위에 3개 이상의 점이 놓여있는 경우를 찾는거에요.

이런 경우를 케이스별로 나누어서 살펴보면 다음과 같아요.


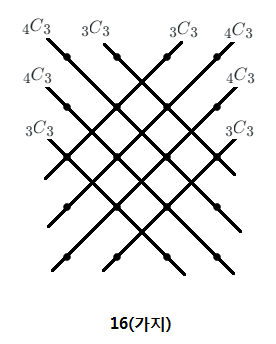
여기까지의 경우의 수를 구하면 왠지 다 구한 것 같은 느낌이 들지만 주의해야할 경우의 수가 있어요. 다음 경우에도 삼각형이 만들어지지 않는답니다. 경우의 수를 찾을 때는 항상 경우의 수가 더 있지 않은지 주의깊게 살펴봐야해요.

이렇게 하여 전체 경우의 수와 삼가형이 만들어지지 않는 경우의 수를 구했으니, 삼각형이 만들어지는 경우의 수를 알 수 있게 되었습니다. 풀이를 정리하면 다음과 같습니다.

이런 문제를 잘 풀기 위해서는 직접 손으로 손을 그어보면서 유형을 나누는 연습이 필요해요.
더 많은 문제를 풀기 위해서는 '모두매쓰' 사이트를 이용하길 추천드립니다.
그럼 오늘도 좋은 하루되시길 바래요~
고등 수학 > 확률과 통계 > 확률의 뜻 > 3개의 점을 선택할 때, 삼각형이 만들어질 확률
'고등 프린트 학습지' 카테고리의 다른 글
| 고등 수학(상) > 평면좌표 > 삼각형의 무게중심의 좌표 G 공식 증명, 연습문제 프린트 학습지 | 무료 PDF 다운로드 (0) | 2024.07.20 |
|---|---|
| 고등 수학 > 수학II > 정적분의 혁신적인 원리 | 무료 PDF 다운로드 (0) | 2024.04.09 |
| 고등 수학 > 확률과통계 > 순열과 조합 > 같은 것이 있는 순열 > 최단 거리로 가는 방법의 수와 그 원리, 프린트 학습지 | 무료 PDF 다운로드 (0) | 2024.02.27 |
| 그래프를 보고 이차함수의 그래프와 직선의 그래프의 판별식, 실근or허근 빈칸 써넣기 프린트 학습지 | 무료 PDF 다운로드 (0) | 2023.11.03 |
| 그래프를 보고 이차함수의 그래프와 x축의 위치 관계 빈칸 써넣기 프린트 학습지 | 무료 PDF 다운로드 (0) | 2023.11.03 |






