고정 헤더 영역
상세 컨텐츠
본문
https://play.google.com/store/apps/details?id=com.clicker.smartnfast&hl=en-KR
Auto Clicker - SmartNFast – Apps on Google Play
Auto Clicker: Tap repeatedly, user-friendly, multiple points.
play.google.com
합집합, 교집합으로 부분집합 구하고 부분집합의 개수 구하기 연습문제


이 문제는 합집합, 교집합으로 집합끼리 포함관계를 찾고, 그것을 이용하여 집합 X의 개수를 찾는 문제입니다.
먼저 X∪A=X를 벤타이어그램으로 한번 표현해보면 포함관계를 쉽게 찾을 수 있어요.
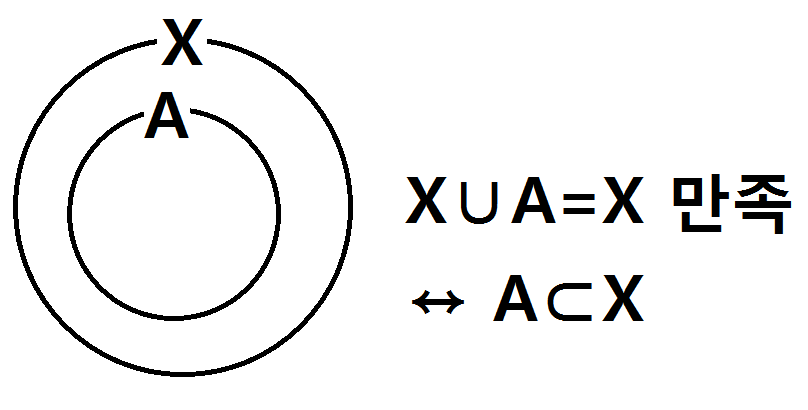
이를 통해 A⊂X 라는 포함관계를 알 수 있어요.
다음으로 X∩B=X를 만족하는 포함관계가 있는 벤다이어그램으로 나타내보면,
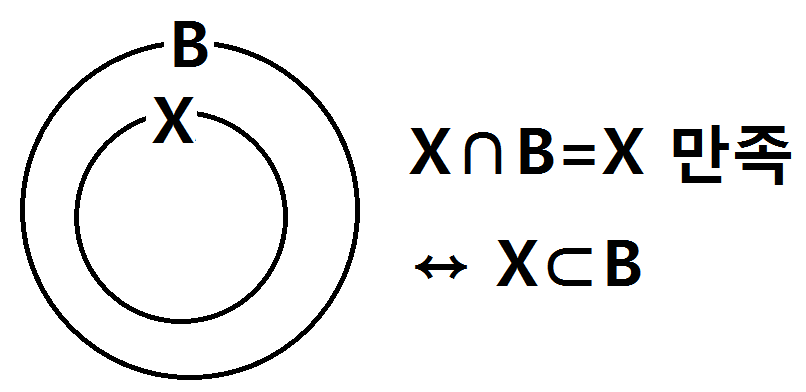
X⊂B 임을 알 수 있어요. 이를 종합해보면, A⊂X⊂B 이므로 집합X는 집합A의 모든 원소를 가지고 있으면서 집합B의 부분집합인 것이죠. 그럼 집합A의 원소의 개수와 집합B의 원소의 개수를 알면 집합X가 가능한 경우를 알 수 있겠습니다.
A={1, 2, 4, 8}, B={1, 2, 4, 8, 16} 이므로
집합X의 개수는 2의 (5-4)제곱 = 2의 1제곱 = 2 입니다.
아래는 풀이식입니다.

이해가 되셨길 바라구요, 혹시 질문이 있거나 이해가 안가는 부분이 있으면 댓글로 남겨주시면 답을 드리겠습니다.
그럼 좋은 하루되세요.
https://play.google.com/store/apps/details?id=com.clicker.smartnfast&hl=en-KR
Auto Clicker - SmartNFast – Apps on Google Play
Auto Clicker: Tap repeatedly, user-friendly, multiple points.
play.google.com
'고등 프린트 학습지' 카테고리의 다른 글
| 명제 p는 q이기 위한 충분조건, 필요조건, 필요충분조건 구하기 연습문제(+절댓값이 포함된 부등식의 해를 구하는 원리) | 무료 PDF 다운로드 (0) | 2023.10.25 |
|---|---|
| 명제 충분조건, 필요조건, 필요충분조건 빈칸 넣기 연습문제 | 무료 PDF 다운로드 (0) | 2023.10.25 |
| 전체집합 U의 두 부분집합 A, B의 특정 영역의 최댓값 또는 최솟값 연습문제 | 무료 PDF 다운로드 (0) | 2023.10.24 |
| 명제 |a|+|b|≥|a+b| 증명 문제 | 무료 PDF 다운로드 (0) | 2023.10.24 |
| 명제 n이 자연수일 때, n제곱이 2의 배수이면 n도 2의 배수이다의 증명 문제 | 무료 PDF 다운로드 (0) | 2023.10.24 |




