고정 헤더 영역
상세 컨텐츠
본문
https://play.google.com/store/apps/details?id=com.clicker.smartnfast&hl=en-KR
Auto Clicker - SmartNFast – Apps on Google Play
Auto Clicker: Tap repeatedly, user-friendly, multiple points.
play.google.com
명제 p는 q이기 위한 충분조건, 필요조건, 필요충분조건 구하기 연습문제


이 문제는 각각의 조건 p와 q를 만족하는 진리집합 P, Q의 포함관계로 충분조건과 필요조건을 찾는 문제입니다.
크게 3가지 유형이 있는데요,
1) P⊂Q 이면 p는 q이기 위한 충분조건
2) Q⊂P 이면 p는 q이기 위한 필요조건
3) P=Q 이면 p는 q이기 위한 필요충분조건
이때 주의해야할 것은 충분조건이라고 말하기 위해서는 P⊂Q 는 참이지만 Q⊂P 는 거짓이어야 한다는거에요. 다시 말해서 충분조건, 필요조건 모두 역인 명제의 참과 거짓도 확인을 해야 한답니다.
진리집합 P와 진리집합 Q의 원소를 보고 포함관계 혹은 일치 여부를 확인하면 됩니다.
(1) 문제에서 절댓값이 등장하는데요, |x| ≤ 3 이 무슨 뜻일까요. |x| 의 정의에 의하면 어떤 수직선이 있을 때, 원점에서부터 x값이 대응되는 점까지의 거리를 나타내요. 그림으로 나타내면 다음과 같아요.

|-3| = 3 이라는 값으로 알고 있죠? 바로 위 그림처럼 0부터 -3까지의 거리가 3이기 때문이랍니다.
그럼 |x| ≤ 3 를 만족하는 x는 무엇일까요? 수직선에서 원점부터 x값이 대응되는 점까지의 거리가 3보다 작거나 같다라는 뜻인데요. 그림을 보면서 이해해볼까요?
자, 질문을 여러번 할 텐데요, 대답을 같이 해볼게요.

|x|=1 을 만족시키는 x값을 구하는 문제가 있다고 해볼게요. 이미 공식처럼 x=1,-1 로 알고 있지만, 정의를 다시 되새기면서 수직선을 보면서 문제를 풀어볼게요. |x|가 무슨 뜻이었죠? 수직선의 원점에서부터 x까지의 거리죠. 그럼 다음 그림에서 x의 위치가 어디인지 알 수 있어요.

위 그림처럼 빨간 점에 x에 대응되면 식을 만족한다는 것을 알 수 있죠. 그러므로 x=1 또는 x=-1 이 |x|=1의 해가 됩니다.
그럼 부등식은 어떻게 풀까요?

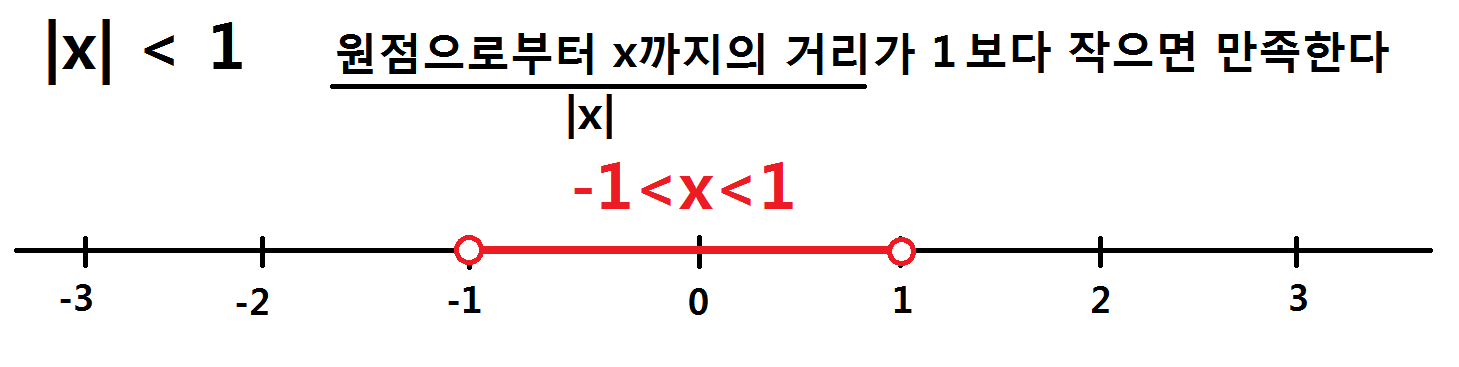
만약 |x|<1 이라는 절댓값이 포함된 부등식을 푼다고 할 때, 위 그림처럼 빨간점의 위치에 x가 있다면 |x|<1 의 해가 될 수 있을까요? 원점으로부터 거리(|x|)가 1보다 작으면 성립하므로 위 그림도 성립하는게 맞아요. 그렇다면 x의 위치가 저 점하나 뿐일까요? 아니겠죠. 다른 점들도 있을거에요.

수직선의 -1보다 크고 1보다 작은 영역의 모든 점들은 |x|<1를 만족하는 x의 값으로서 콕 집어서 해를 말할 수 없기 때문에 부등식으로 해를 나타내면 다음과 같아요.
이런 원리에 의하여 |x|≤3 을 수직선에 나타내보면 다음과 같아요.

이렇게 |x|≤3 이 -3 ≤x ≤3 이 되는 과정을 눈으로 직접 보면서 확인해보았어요.
개념을 설명하다보니 내용이 많이 길어졌는데요,
아래는 문제 풀이입니다.


이해가 잘 되셨길 바라구요, 혹시 이해가 안가는 부분이 있으시면 댓글로 남겨주세요~
좋은 하루되세요~
https://play.google.com/store/apps/details?id=com.clicker.smartnfast&hl=en-KR
Auto Clicker - SmartNFast – Apps on Google Play
Auto Clicker: Tap repeatedly, user-friendly, multiple points.
play.google.com
'고등 프린트 학습지' 카테고리의 다른 글
| 집합 A=B 일 때, 미지수 구하기 연습문제 프린트 학습지 | 무료 PDF 다운로드 (0) | 2023.10.26 |
|---|---|
| 부등식에 미지수가 포함된 충분조건, 필요조건 연습문제 | 무료 PDF 다운로드 (0) | 2023.10.26 |
| 명제 충분조건, 필요조건, 필요충분조건 빈칸 넣기 연습문제 | 무료 PDF 다운로드 (0) | 2023.10.25 |
| 합집합, 교집합으로 부분집합 구하고 부분집합의 개수 구하기 연습문제 | 무료 PDF 다운로드 (0) | 2023.10.25 |
| 전체집합 U의 두 부분집합 A, B의 특정 영역의 최댓값 또는 최솟값 연습문제 | 무료 PDF 다운로드 (0) | 2023.10.24 |




