고정 헤더 영역
상세 컨텐츠
본문
https://play.google.com/store/apps/details?id=com.clicker.smartnfast&hl=en-KR
Auto Clicker - SmartNFast – Apps on Google Play
Auto Clicker: Tap repeatedly, user-friendly, multiple points.
play.google.com
전체집합 U의 두 부분집합 A, B의 특정 영역의 최댓값 또는 최솟값 연습문제


이 문제는 고등학교 내신시험에 빠지지 않고 등장하는 문제입니다.
이 문제에서는 다음 그림과 같은 영역의 최댓값과 최솟값을 물어보고 있어요.

이런 질문을 할 수 있죠.
'당연히 두 집합의 교집합인 저 영역은 0보다 항상 크겠지?'
이 질문에 대한 대답은 다음 그림일 경우에는 틀린게 됩니다.

이렇듯 교집합이 없을 수가 있어요. 그럼 이런 질문도 가능하겠네요.
'그럼 두 집합의 교집합이 없는 경우는 무조건 있겠지?'
이 질문에 대한 대답도 집합 U의 원소 개수와 집합 A, B의 원소 개수에 따라 달라 질 수 있어요.
특히 이 문제에서는 전체 학생 수가 37명이고 A영화를 본 학생이 22명, B영화를 본 학생이 24명이기 때문에 만약 위 그림과 같다면 모순이 발생하죠.

만약 위 그림처럼 교집합이 없는 그림이라면 말도 안되는 경우가 생겨요. A 영화와 B 영화를 본 학생을 합하면 전체 학생 수를 넘어버리게 되니까요. (유령이 봤을리가..)
여기서 굉장히 중요한 점을 발견했어요! 바로 이런 경우에 반드시 A 영화와 B 영화를 모두 본 학생이 반드시 존재한다는 사실이죠. 이 문제의 경우에는 그렇단 말이죠. 중요한 단서입니다. 그럼 몇 명일 때 가장 작을까요.

물리적인 힘을 가해볼까요? 집합 A와 집합 B를 최대한 멀리 떨어뜨리는 힘을 가해봅시다!

근데 실제로 집합 A와 집합 B의 크기가 상당히 클 수 있어요. 그럴 때 집합 U의 벽에 부딪히겠죠?
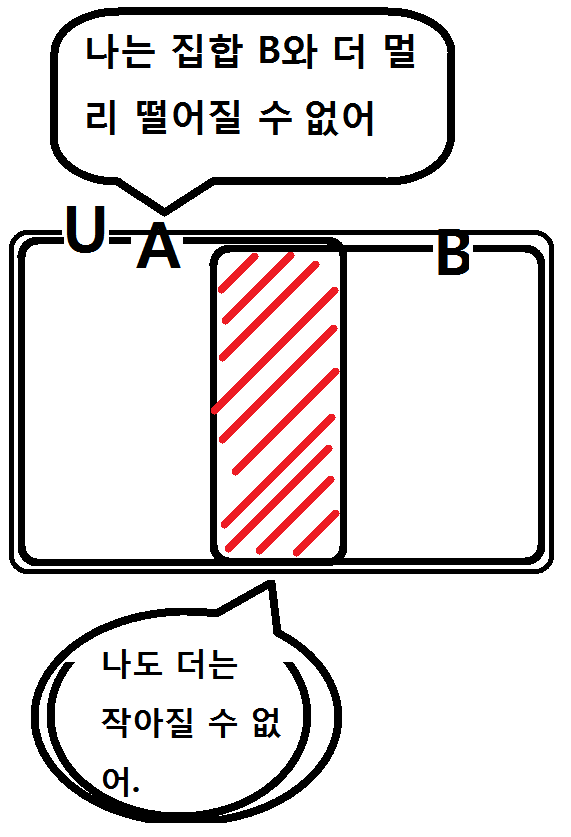
집합 A와 집합 B의 원소의 개수가 정해져있기 때문에 만약 원소의 개수만큼 자리를 차지한다면 위 그림처럼 더 이상 집합 A와 집합 B가 멀리 떨어질 수 없을거에요. 최대한 멀리 떨어진 상태가 바로 집합 A와 집합 A의 교집합인 n(A∩B)의 원소의 개수가 최소일 때랍니다! 다르게 말하면 두 집합 A, B의 합집합이 가장 클 때이죠!
그럼 집합 A, B의 교집합이 최소일 때의 원소의 개수는 몇인지 계산해봐요. 저 그림에 답이 있어요!
n(A∪B)=n(A)+n(B)-n(A∩B)에 값을 대입해보면
37=22+24-x 이므로
x = 46-37 =9 이예요. 그림을 그렸는데 최솟값을 구했네요.
이번에는 최댓값을 구해봐요. 역시 그림에 물리법칙을 적용해볼까요? 이번에는 교집합의 원소의 개수가 많아야 하니까 집합 A와 집합 B를 최대한 겹치게 만들어야해요.
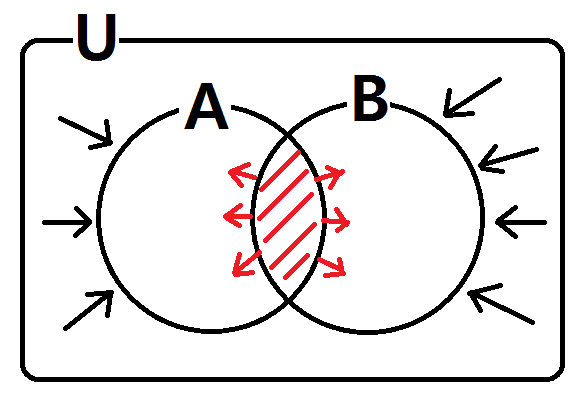

이 문제에서는 집합 A의 원소의 개수가 22, 집합 B의 원소의 개수가 24이므로 최대한 교집합을 늘려가다보면 결국 집합 A가 집합 B의 부분집합이 되는 경우의 그림을 생각할 수 있어요. 바로 이때가 교집합이 최대가 되는 때랍니다. 집합 A와 집합 B의 합집합을 바라보면 이때가 합집합이 가장 작을 때라는 것도 아시길 바래요.
이제 바로 최댓값을 구하러 가볼게요.
n(A∪B)=n(A)+n(B)-n(A∩B)에 값을 대입해보면
24 = 22+24-x 이므로
x = 46-24 = 22 이예요. 이 값이 x의 최댓값이랍니다.
그럼 x의 최댓값과 최솟값의 합은 9 + 22 = 31 이 정답입니다.
수학 문제를 푸는데 왜 물리법칙을 썼을까요? 사실 물리적인 법칙은 수학에 있을 수 없어요. 다만 수학에는 면적이라는 개념이 있지요. 사실은 원소의 개수를 면적으로 사용해서 풀었다고 보시면 됩니다.
아래 풀이는 이러한 풀이를 수식으로 정리한거예요. 아래처럼 풀어도되고, 위처럼 생각하며 풀어도 좋습니다.

이해가 되었길 바라구요, 혹시 질문이 있거나 이해가 안가는 부분이 있으면 댓글로 남겨주시면 답을 드리겠습니다.
그럼 좋은 하루되세요.
https://play.google.com/store/apps/details?id=com.clicker.smartnfast&hl=en-KR
Auto Clicker - SmartNFast – Apps on Google Play
Auto Clicker: Tap repeatedly, user-friendly, multiple points.
play.google.com
'고등 프린트 학습지' 카테고리의 다른 글
| 명제 충분조건, 필요조건, 필요충분조건 빈칸 넣기 연습문제 | 무료 PDF 다운로드 (0) | 2023.10.25 |
|---|---|
| 합집합, 교집합으로 부분집합 구하고 부분집합의 개수 구하기 연습문제 | 무료 PDF 다운로드 (0) | 2023.10.25 |
| 명제 |a|+|b|≥|a+b| 증명 문제 | 무료 PDF 다운로드 (0) | 2023.10.24 |
| 명제 n이 자연수일 때, n제곱이 2의 배수이면 n도 2의 배수이다의 증명 문제 | 무료 PDF 다운로드 (0) | 2023.10.24 |
| 자연수 k의 배수의 집합 - 부분집합, 교집합, 합집합 연습문제 프린트 학습지 | 무료 PDF 다운로드 (0) | 2023.10.24 |




