고정 헤더 영역
상세 컨텐츠
본문
https://play.google.com/store/apps/details?id=com.clicker.smartnfast&hl=en-KR
Auto Clicker - SmartNFast – Apps on Google Play
Auto Clicker: Tap repeatedly, user-friendly, multiple points.
play.google.com
부등식에 미지수가 포함된 충분조건, 필요조건 연습문제


많은 학생들이 헷갈리거나 어려워하는 문제인데요, 두 조건을 수직선에 나타낼 때, a를 어디에 써야할지부터 막막하거나, a의 위치가 과연 어느 범위에 가능한지 매우 세밀하게 살펴봐야하는 문제기 때문입니다.
우선 위 문제를 수직선 상에 나타내면 다음 그림과 같아요.
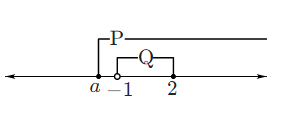
문제의 조건은 'p는 q이기 위한 필요조건이다'는 건데요, 진리집합 Q가 진리집합 P에 포함되어야 해요. 그래서 위 그림처럼 집합 P가 집합 Q를 감싸는 모양으로 그린거죠.
그런데 a는 포함된 점인데 비해서 -1은 포함되지 않은 점이에요. 그렇다면 과연 a가 좌우로 움직일 수 있을 때, -1까지 위치할 수 있을까요? 이것이 정답을 결정하기 때문에 잘 살펴봐야합니다. 관건은 a가 -1에 위치할 때, 집합 Q의 모든 원소게 집합 P에 포함되는가예요.
어떨까요? 네 가능하죠. 왜냐하면 집합 Q에 -1은 사실 없는 원소니까요. a가 -1에 위치하더라도 집합 P는 집합 Q의 모든 원소를 가지게 되니 조건을 만족합니다.
어떤 점은 포함되고 어떤 점은 포함되지 않는데, 그래봤자 4가지 경우가 전부예요. 점은 2개 뿐이니까요.

세번째 그림이 안되는 이유는 점 a의 위치가 좌우로 이동할 수 있지만 점 b의 위치와 같아지면 집합 Q가 가지고 있는 원소 b를 집합 P는 가지지 못하기 때문에(집합 P는 원소 a를 포함하지 않음) 집합 Q가 집합 P에 포함되지 않아요.
포함관계를 살펴볼때 위처럼 사고하는 과정이 필요하답니다.
그럼 도움이 되셨길 바라고, 궁금하신게 있으면 댓글로 남겨주세요.
좋은 하루되세요~
https://play.google.com/store/apps/details?id=com.clicker.smartnfast&hl=en-KR
Auto Clicker - SmartNFast – Apps on Google Play
Auto Clicker: Tap repeatedly, user-friendly, multiple points.
play.google.com
'고등 프린트 학습지' 카테고리의 다른 글
| 일차함수의 역함수 구하기 연습문제 프린트 학습지 | 무료 PDF 다운로드 (0) | 2023.10.26 |
|---|---|
| 집합 A=B 일 때, 미지수 구하기 연습문제 프린트 학습지 | 무료 PDF 다운로드 (0) | 2023.10.26 |
| 명제 p는 q이기 위한 충분조건, 필요조건, 필요충분조건 구하기 연습문제(+절댓값이 포함된 부등식의 해를 구하는 원리) | 무료 PDF 다운로드 (0) | 2023.10.25 |
| 명제 충분조건, 필요조건, 필요충분조건 빈칸 넣기 연습문제 | 무료 PDF 다운로드 (0) | 2023.10.25 |
| 합집합, 교집합으로 부분집합 구하고 부분집합의 개수 구하기 연습문제 | 무료 PDF 다운로드 (0) | 2023.10.25 |




