고정 헤더 영역
상세 컨텐츠
본문
수학II를 잘하기 위해서는 삼차함수 또는 사차함수의 그래프의 개형을 정리하는 것이 무엇보다 중요해요. 그래프의 개형에 대해 알지 못하면 응용된 고난이도 문제를 접근하거나 파악하는데 어려움을 겪게 되거든요. 또한 수학II 전체에 대해 정말로 깊이 있는 이해를 하려면 사차함수의 그래프 개형에 대해 정리가 잘 되어 있어야 합니다. 사차함수의 그래프의 개형은 총4가지예요. 사(4)차함수니까 4개 이렇게 외워도 좋아요. 참고로 삼(3)차함수의 그래프 개형은 3가지예요.
여기서는 사차함수의 개형이 4개라는 것을 외우는 것으로 그치지 않고 왜 4개의 개형이 나오는지도 이해하면서 정리하도록 할게요.
도함수의 활용
사차함수의 그래프 단원의 이름이 왜 도함수의 활용일까요.
함수 f(x)의 도함수는 f'(x)인데요, 바로 그래프의 개형을 파악하는데 f'(x)를 활용라는 뜻이에요. 그럼 f'(x)가 무엇인지 정확히 알아야 활용도 할 수 있는 거겠죠.
f'(x)는 임의의 x에 대하여 그래프 위의 점 (x, f(x))에서 그은 접선의 기울기값이에요.
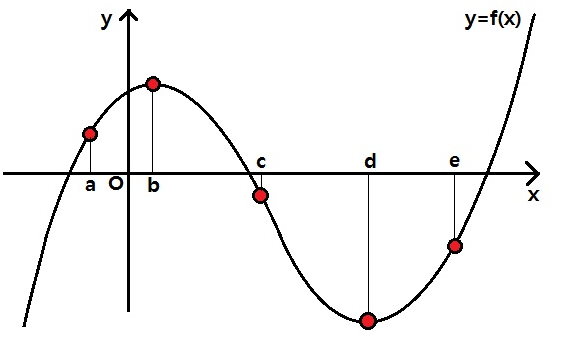
만일 x=a, x=b, x=c, x=d, x=e 라는 다섯 개의 x값이 있을 때 그래프 위의 점은 위와 같아요.
이때 그 점을 접하는 직선(접선)을 긋게 되면 접선의 기울기값이 존재하는데 그게 바로 도함수 f '(x)에 x값을 대입한 값이 되는 거죠.
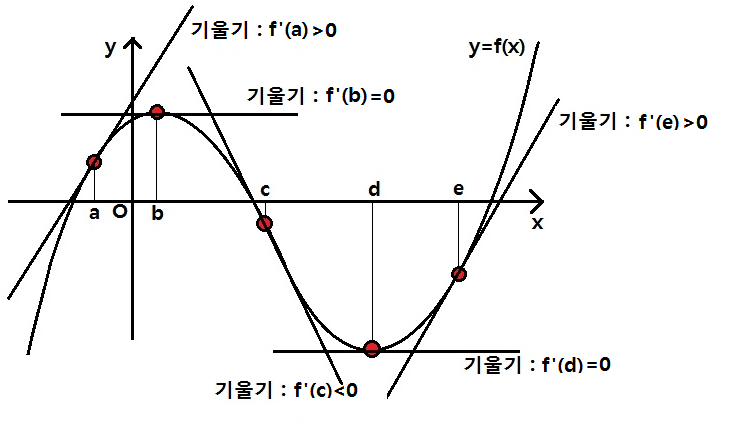
여기서 기울기의 값이 0이 되는 것에 주목할 필요가 있어요. 위의 그림에서는 접선의 기울기가 0이 되는 접점의 x좌표가 x=b, x=d인 경우인데요, 이 점이 극대 , 극소라는 점이에요. 바로 이 점을 찾아야만 그래프를 가장 빠르게 그릴 수 있게 됩니다.
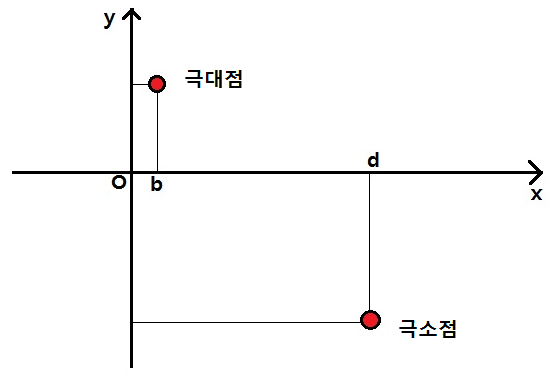
함수의 그래프를 그릴 때 극대 극소를 먼저 찾는다
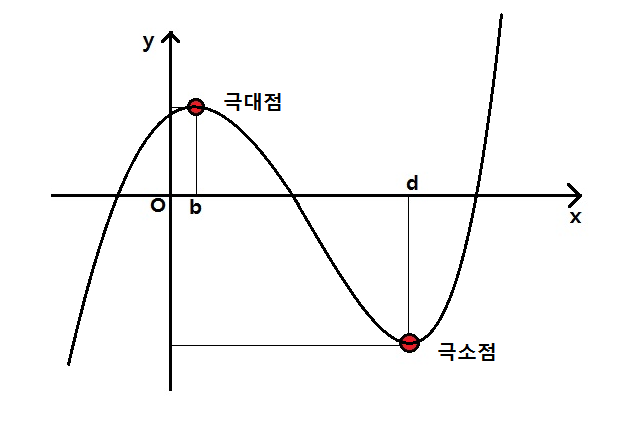
이렇게 극대점 또는 극솟점을 찾을 수 있는 방법이 f'(x)=0 (f'(x) 즉 기울기값이 0과 같은 x를 구하시오)를 푸는거에요.
이처럼 f'(x)=0의 근의 종류는 함수의 그래프 개형을 구하는 기준이 되는 매우 중요한 식이에요.
삼차방정식 f'(x)=0 의 근의 종류가 곧 개형의 종류
사차함수를 미분하게 되면 한 차수가 낮은 삼차함수가 돼요. 그러면 f'(x)=0는 삼차방정식이 되는데요, 삼차방정식의 실근의 종류가 곧 극대, 또는 극소와 함께 함수의 그래프 개형을 결정짓는거에요.
따라서 f'(x)=0를 그래프로 해석해서 어떤 종류의 해가 있는지 살펴보면 4가지 유형이 있음을 알 수 있습니다.
아래는 4가지 개형을 하나로 모아 정리한 그림이에요.
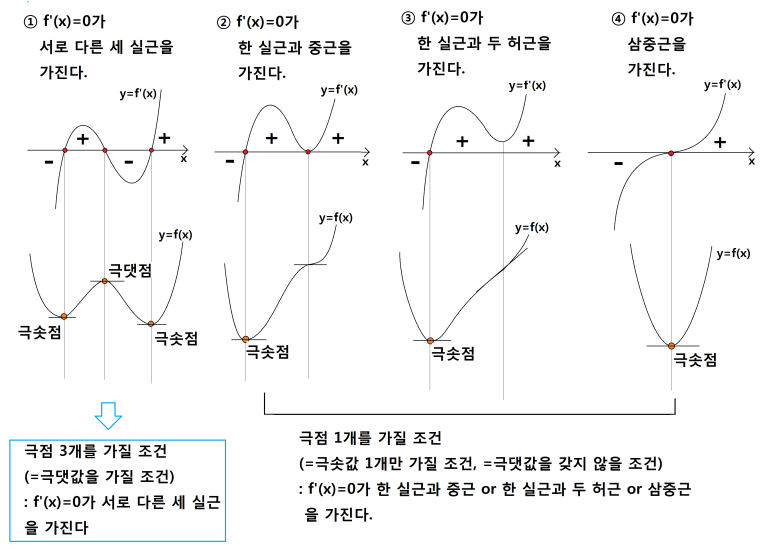
그래프 극대와 극소는 f'(x)=0일 뿐만 아니라 x값 주변에서 f'(x)의 값의 부호가 바뀌어야 한다는 조건도 가져야 하므로 두번째 유형에서 극값이 1개뿐이라는 것도 주의하시길 바래요.
또 사차함수의 최고차항의 계수가 음수인 경우에는 x축을 기준으로 상하가 뒤집히는 모양의 그래프가 나오므로 극솟값이 극댓값으로, 극댓값이 극솟값으로 바뀌니 다른 유형으로 따로 외울 필요가 없어요.
그리고 가장 중요한 것은 직접 그래프를 그리면서 개형을 파악하는 연습이에요. 모두매쓰 사이트에서 문제를 생성해서 그래프 그리는 연습에 활용하길 바래요.
'고등 프린트 학습지' 카테고리의 다른 글
| 절댓값 기호가 포함된 이차함수의 그래프 연습문제 프린트 PDF (0) | 2022.10.20 |
|---|---|
| 절댓값 기호를 포함한 일차함수의 그래프, y=|f(x)|,y=f(|x|),|y|=f(x),|y|=f(|x|)꼴 연습문제 프린트 PDF (0) | 2022.10.20 |
| 수학II > 도함수의 활용 > 삼차함수, 사차함수의 극대 극소를 찾는 이유와 극대 극소를 구하지 않으면 생기는 일 (0) | 2022.10.17 |
| 수학II > 도함수의 활용 > 삼차함수의 그래프 개형 3가지, f'(x)=0 의 실근이 특별한 이유 (0) | 2022.10.17 |
| 수학I > 수열 > 수학적 귀납법이 도미노와 같은 이유 (0) | 2022.10.17 |






