고정 헤더 영역
상세 컨텐츠
본문


첫번째 도미노가 쓰러지면 '도미노의 작동원리'에 따라서 계속해서 다음 도미노가 쓰러지게 돼죠.
이 도미노 게임의 작동원리가 무엇일까요. 그건 바로
앞의 도미노가 쓰러지면 다음 도미노가 쓰러진다
입니다. 이것을 그대로 명제의 증명법에 적용하는 것이 수학적 귀납법이예요.

이것만 증명하면 됩니다. 이것을 저는 '논리적 기계'라고 불러요. 이 기계가 위 그림처럼 작동한다는 것을 증명만 하면 나머지는 이제 k에 어떤 값만 대입하면 되는거거든요.
가령 위 논리적 기계가 도미노처럼 작동한다는 것을 증명한 상태에서 만약 k=1을 대입할 때 참이 되기만 한다면 논리적 기계에 의해 k=2일 때도 참이 되죠. 그럼 또 k=2를 이 기계에 대입하면 k=3이 참이 되는 거에요. 그러면 '모든 자연수'에 대하여 참임이 증명이 되는거에요.
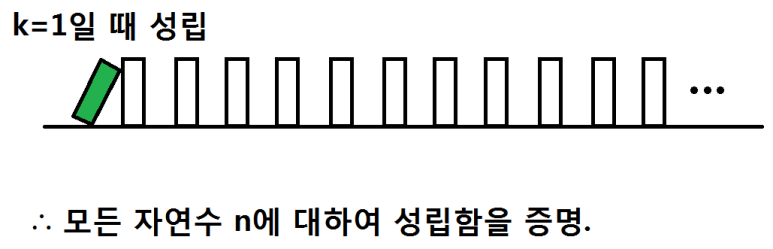
이게 수학적 귀납법의 핵심이에요. 어떤 명제가 저 두 개의 도미노(k와 k+1)의 작동원리를 그대로 따른다면 수학적 귀납법으로서 증명이 참으로서 끝난거에요. 우리들은 바로 저 두 개의 도미노의 작동원리가 명제에 그대로 적용되는지만 논리적인 절차에 따라 확인해주면 되는겁니다.
만약 앞의 도미노가 안 쓰러지면? 그건 아예 고려조차 하지 않아요. 오직 앞의 도미노가 쓰러질 때 다음 도미노도 쓰러지는가?만 생각하는게 수학적 귀납법적 사고방식이예요. 도미노는 이미 이러한 방식으로 작동하지만, 어떤 명제가 이렇게 작동하는지는 하나씩 살펴봐야하는거죠.
어떤 명제 하나의 가지고 와서 직접 증명하며 설명해볼게요.
모든 자연수 n에 대하여 다음 명제가 성립함을 수학적 귀납법으로 증명하시오.
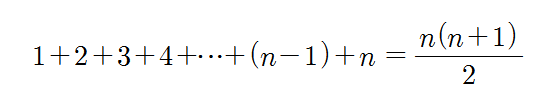
모든 자연수에 대하여 성립하는지 어떻게 알까요. 위 식에 1, 2, 3, 4 등을 대입해보면 참이되는걸 알 수 있지만, 모든 자연수를 넣을 수는 없으니까요.
이미 수열의 합 공식을 알고 있는 학생은 너무 당연한거 아니야? 이 당연한 걸 왜 또 증명해? 라고 생각할 수 있어요. 하지만 1부터 n까지의 합은 n(n+1)/2와 같다는 것을 '수학적 귀납법'으로써 증명하지는 않았던 거지요. 그럼 수학적 귀납법으로 증명을 시도해보겠습니다.
수학적 귀납법은 딱 1가지만 증명하면 돼요.
n=k일 때 성립하면(가정), n=k+1일 때에도 성립
n=k와 n=k+1의 연결고리만 성립한다는 걸 증명하기만 하면 되요.

이것을 일단 '참'이다라고 가정하는거에요. 그런 후에
n이 k일 때에 성립할 때 n이 k+1일 때에도 성립한다.
마치 도미노 그림처럼, 앞의 도미노(n=k)가 쓰러지면 다음 도미노(n=k+1)도 쓰러짐을 증명해야해요.
여기서 핵심은 무엇이냐면,
n=k일 때 성립하는지가 중요한 것이 아니라, n=k일 때 성립한다면 n=k+1일 때에도 반드시 성립하는지 증명하라는 거에요.
그럼 어떻게 증명하는지 살펴볼게요.

위 식의 양변에 k+1을 더해요.

등식의 성질을 이용했기 때문에 n=k일 때 참이라고 가정했으므로 위 식도 참이라는 걸 알 수 있어요. 그럼 이 식을 약간 정리해볼게요.

이걸로 n=k 일때와 n=k+1 일때의 연결고리가 생겼어요. 이것으로서 다음과 같은 문장이 증명된거에요.
n에 k를 대입했을 때 성립한다면, n에 k+1을 대입해도 성립한다
이제 모든 자연수에 대해 성립한다는 것은 k=1을 대입하고 그것이 성립하는지만 확인하는 것으로 마무리 됩니다.
마치 도미노의 맨 앞의 막대기를 쓰러뜨리는 것과 같은거지요.
k=1을 대입하게 되면
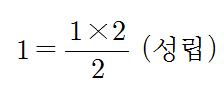
이와 같이 성립한다는 것을 알 수 있어요. 그러면 이러한 논리적 기계는 다음 수인 2도, 3도, 4도 참으로 만들어 줄 거에요. 결국 모든 자연수에 대하여 성립함을 증명한 것이죠.
이렇게 수학적 귀납법으로 명제 하나를 참임을 증명했는데요, 수학적 귀납법의 핵심은 바로 도미노와 같은 작동원리를 가지는지를 증명한다는 거에요. 바로 앞의 도미노가 쓰러지면 다음 도미노도 쓰러진다는 논리요. 그런다음에 맨 앞의 도미노인 1을 쓰러뜨기만 하면 되는 이치입니다.
'고등 프린트 학습지' 카테고리의 다른 글
| 수학II > 도함수의 활용 > 삼차함수, 사차함수의 극대 극소를 찾는 이유와 극대 극소를 구하지 않으면 생기는 일 (0) | 2022.10.17 |
|---|---|
| 수학II > 도함수의 활용 > 삼차함수의 그래프 개형 3가지, f'(x)=0 의 실근이 특별한 이유 (0) | 2022.10.17 |
| 수학(상) > 이차방정식의 근의 공식 증명(유도과정) + 이차방정식 문제 프린트 학습지 (1) | 2022.10.14 |
| 수학(상) > 이차방정식 문제 - 프린트 학습지 (0) | 2022.10.13 |
| 수학(상) > 이차방정식 근의 공식 적용 문제 - 프린트 학습지 (0) | 2022.10.13 |






