고정 헤더 영역
상세 컨텐츠
본문
일차방정식의 활용에서 소금물의 농도 문제는 굉장히 유명한데요,
왜 많은 학생들이 소금물의 농도 문제를 어려워할까요.
그 이유는 바로 '비율'과 '백분율'에 대한 개념이 잘 자리잡혀 있지 않아서 예요.
초등수학에서 다루는 '비와 비율'에 대한 이야기를 잠시 먼저 하고, 소금물 농도 문제를 다뤄볼까해요.
비
비는 한자말이에요. 비(比)는 견주다. 비교하다. 라는 뜻이 있어요. 그러니 당연히 2가지의 값이 비교되도록 와야 하겠죠.

만일 2개의 선분이 있다고 하면 길이를 비교할 수가 있는데요, 길이를 비교해보면 왼쪽의 선분과 오른쪽의 선분의 길이가
1 : 2
의 비로 나타낼 수 있어요. '비'라는 것은 이처럼 두 가지의 값을 비교하며 나타내는 좋은 표현 방법이에요.
그런데, 여기서 '비'를 하나의 값으로 표현하는 방법을 생각했어요. 그것이 '비율'이에요.
비율
비율은 비의 왼쪽 값을 분자, 비의 오른쪽 값을 분모에 놓고 하나의 분수로 나타내는 표현 방법을 뜻해요.

비와 비율은 표현 방법만 다른 것 뿐이랍니다. 수학 용어에는 끝에 '율'이 들어가는 경우가 많은데요, 비율을 줄여쓴 말이라고 보면 돼요. 율이 들어가는 수학 용어에서 대표적인 것이 바로 백분율이에요. (고등수학에서 나오는 평균변화'율'의 율도 비율을 줄인말이랍니다)
백분율
백분율은 말그대로
백분 + 율
이에요. 백분은 말그대로 100을 전체의 값으로 본다는 뜻이에요. 백분율은 다음과 같이 정의할 수 있어요
백분율(%) = 비율 × 100
어떤 수에 비율을 곱한다는 것은 무슨 의미일까요. 그 어떤 수를 '전체'로 본다는 뜻이에요.
예를 들어 학생수가 400명인 학교가 있다고 해볼게요. 이 학교의 0.2 의 비율로 안경을 쓴다고 하면 몇 명이 안경을 쓴 걸까요.
400 × 0.2 = 80
80명이 안경을 썼다고 할 수 있어요. 비율은 전체값에 곱하여서 해당하는 비율만큼의 수를 찾아낼 때 사용한답니다. 이 문제에서는 400을 전체의 값으로 보고 비율인 0.2를 곱해서 0.2 비율만큼의 값인 80이 나온거에요.
그런데 전체의 값을 100으로 하는 것을 특별히 '백분율'이라고 명칭하고, 사용하기 시작한거에요. 왜냐하면 사람들이 100이라는 수를 놓고 어떤 비율을 말하는 것을 더 쉽게 느끼기 때문이에요. 한마디로 비율을 사람들에게 말할 때 소수점으로 된 수는 어려우니 100을 곱해서 말하고 그걸 백분율이라고 한거죠.

비율에 100을 곱한다는 것은 100을 전체값으로 본다는 뜻이며 이것을 백분율이라고 해요.
그럼 이제 소금물의 농도 이야기를 해볼게요. 소금물의 농도의 단위가 %이기 때문에
소금물의 농도도 백분율의 구조라는 것을 알 수 있어요.
소금물의 농도 = 비율 × 100
일단 식의 구조를 보면 비율에 100을 곱한 식이 돼요. 그럼 이제 비율이 무엇인지만 알면 공식을 알 수 있어요.
비율을 구성하는 2가지 값이 무엇일까요. 여기서는 소금의 양 : 소금물의 양 이에요. 따라서 이를 비율로 나타내면
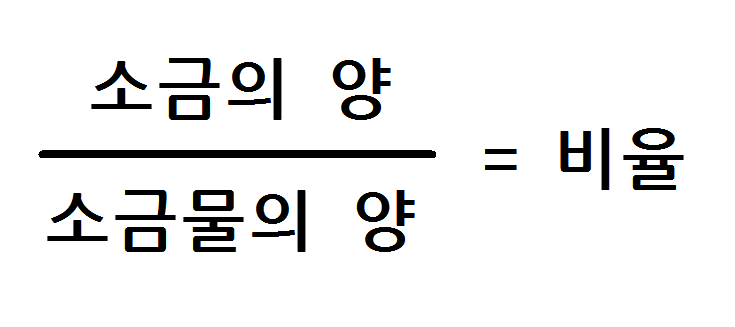
그렇다면 소금물의 농도 공식은 바로 이 비율에 100을 곱한 식이 되는 거에요.

만약 농도가 30%라면 소금물이 100g일 때 소금이 30g 을 차지한다는 뜻이랍니다. 사람들은 비율을 %로 말해야 더 쉽게 인식하기 때문이죠. 비율에 100을 곱한 것. 그게 백분율이고 %라는 단위를 사용한다고 정리할 수 있어요.
농도 공식이 왜 저렇게 생겼는지 이제 이해할 수 있겠죠? 자 그렇다면 이제 두 번째 공식인 소금의 양 공식에 대해 살펴볼게요.
소금의 양 공식은 위에서 말한 소금물의 농도 공식을 변형한 것에 불과해요.

이렇게 소금의 양 공식은 소금물의 농도 공식에서 나온거랍니다.
소금의 양 공식은 너무나도 중요해요. 왜냐하면 소금물의 농도 문제는 사실 소금의 양 공식으로 99% 해결할 수 있기 때문이에요.
일단 소금물의 농도 문제를 풀기 위한 사전 지식으로서 '비와 비율' 그리고 '백분율'에 대해 공부하고, 백분율로 이루어진 소금물의 농도, 그리고 소금물의 양 공식에 대해서 살펴봤어요.
설명이 길어질 것 같으니 다음 소금물 문제 유형편에서 다루어 보도록 할게요.
'중등 프린트 학습지' 카테고리의 다른 글
| 중1 수학 > 일차방정식의 활용 > 원가, 정가, 이익의 개념 (0) | 2022.10.13 |
|---|---|
| 중1 수학 > 일차방정식의 활용 > 소금물 문제(소금물에 소금 더 넣기) + 프린트 학습지 (0) | 2022.10.11 |
| 중3 수학 > 제곱근의 계산⑤ - 대소비교 프린트 학습지 (0) | 2022.10.09 |
| 중3 수학 > 제곱근의 계산③ - 정수부분 구하기 프린트 학습지 (0) | 2022.10.09 |
| 중3 수학 > 제곱근의 계산② - 간단히 하기 프린트 학습지 PDF (0) | 2022.10.09 |






