수학II > 미분 > 미분계수의 정의, 미적분 개념의 시작

미분이라는 것을 이야기하려면 '기울기'(평균변화율)에 대한 개념이 있어야 해요.

기울기를 중학교 2학년 때 배우죠. 바로 일차함수라는 단원에서요.

일차함수식을 살펴보면

이렇게 x에 대한 일차항이 있는데요, a가 바로 기울기의 값을 나타내고 있어요. 기울기의 정의가 뭐였는지 알아봐요.

미분에 대해 설명하는데 왜 기울기 이야기가 나오는지 궁금하실텐데요. 미분 개념에서 가장 중요한 것이 기울기라는 개념이기 때문이에요. 미분을 구성하는 요소를 그림으로 나타내면 다음과 같아요.

기울기(다른 말로 평균변화율)에 대해 함수의 그래프와 함께 이야기를 계속 해볼게요.

y=f(x) 위에 2개의 점이 있다고 할게요. 이 두 점을 지나는 직선과 직선의 기울기를 구하면

이렇게 두 점의 평균변화율(기울기)를 식으로 나타내는데 성공했어요. 그런데 이게 미분하고 무슨 관계가 있을까요. 미분은 그냥 기울기식이에요. 딱 한가지만 달라요. 그게 뭐냐면 바로 '극한' 개념이 포함된다는 거에요.

극한이 뭐냐고 물어본다면, 직관적으로 설명할 수 밖에 없는데요, 그게 고등학교 과정에서 지향하는 학습목표기도 해요.

극한이라는 건 '한없이 ~되는 상태'라고 생각하면 돼요. 끝없이 ~되고 있는 상태라고 봐도 되요. 이러한 관념을 위 그림에 대입시켜보겠습니다.

두 개의 점 중에서 오른쪽에 있는 점을 그래프를 따라서 왼쪽에 있는 점에 극한으로 보내면 어떤 모습일까요.

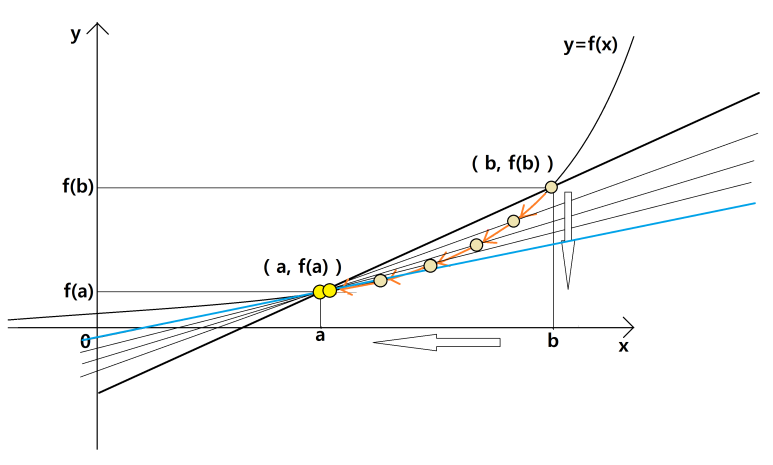
오른쪽의 점이 왼쪽에 있는 점에 '한없이 가까이 다가갈 때' 두 점의 기울기값이 바로 미분계수예요.

여기서 한없이 다가간다면 두 점은 만난 것일까요 안 만난 것일까요. 이 부분이 한 번 생각할 만한 부분이에요. 고등학교 수학에서는 마치 만나지 못할 것 같은 뉘앙스를 풍기는데 대학 수학에서는 이미 만난 것을 증명해버렸으니까요. 그래도 이러한 직관적인 이해가 학습에 중요한 역할을 합니다.

이러한 직관적인 이해를 먼저 하는게 우선이구요, 다음으로 이것을 식으로 나타내는 부분만 하면 미분 개념이 끝이 납니다.

오른쪽 점의 x값인 b가 왼쪽 점의 x값인 a에 한 없이 가까이 간다는 것은 극한 개념인 lim(리미트라고 읽음) b → a 로 표현할 수 있어요. 이때 기울기의 값은 그때그때마다 변하는 거죠. 결국 이 기울기는 x=a에서의 접선의 기울기값이 되고 이를 미분계수라고 불러요.

이때 b-a=h 라고 치환하게 되면 미분계수의 식이 다음처럼 변형돼요.

이를 x=a에서의 미분계수라고 하고 짧게 f'(a)로 표현해요.

앞으로 미분계수를 f'(에프 프라임이라고 읽음)이라고 명칭하고 이것은 그래프상의 접선의 기울기값으로 사용하게 되는거죠.

식이 복잡해보이지만 결국 미분은 접선의 기울기를 나타내는 값이고, 극한 + 기울기라고 할 수 있어요.

이것이 발전된 게 도함수의 정의입니다.